背景说明
Logistic回归开发的评分卡模型主要用于信贷产品的申请(Application)和贷后(Behavior)环节。
- 优势:可解释性、稳定性
- 劣势:准确率不及深度学习
模型开发流程
- 检查数据
- 单变量检查
- 变量间逻辑关系检查
- 设计模型
- 时间窗口选定
- 行为表现定义
- 衍生变量
- 基于原始变量衍生一系列建模变量
- 抽样与设置权重
- 随机抽样
- 设置权重
- Train & Test
- 细分箱
- 变量细分箱
- 计算WOE值与IV
- 变量筛选
- 删除IV值较低的变量
- 删除与业务含义不符的变量
- 粗分箱
- 细分箱合并为粗分箱
- 转换WOE值
- 各变量分箱栏位原始值转换为WOE值
- Logistic回归
- 拟合模型参数
- 评分标准化
- 计算各变量分箱栏位对应得分
- 验证模型
- 模型区分能力
- 模型排序性
- 模型稳定性
- 模型部署上线
检查数据
- Garbage in, garbage out. 第一步永远是进行数据检查与分析。
- 需要良好的沟通能力去与业务部门、数据库等部门进行沟通
- 此过程有利于对业务发展、业务特点进行理解,有利于后续的建模工作
单变量检查
- 所有的原始变量都需要检查,如:还款月份、申请时间、还款频率、逾期状态等。
变量间逻辑检查
- 单个变量时间逻辑检查。如:逾期状态前后滚动的跳跃情况,上月逾期M1,本月不可能逾期M4
- 多个变量间的逻辑检查。如:贷款申请月份+贷款期限=贷款结束时间。
数据分布
- 总量、缺失量、缺失占比
- 均值、中值、标准差、最小值、最大值与各分位点值
数据处理
- 奇异值、极端值、缺失值处理。(评分卡式建模无需处理)
设计模型
定义表现
滚动率(Roil Rate)分析:统计账户从上个月的逾期状态变动到这个月的逾期状态的占比情况,寻找占比稳定的逾期状态。一般当逾期占比大于50%时,可以将该逾期定义为坏。传统银行的坏定义在逾期四期及以上(M4和M4+),互联网产品根据产品的实际情况会短很多。
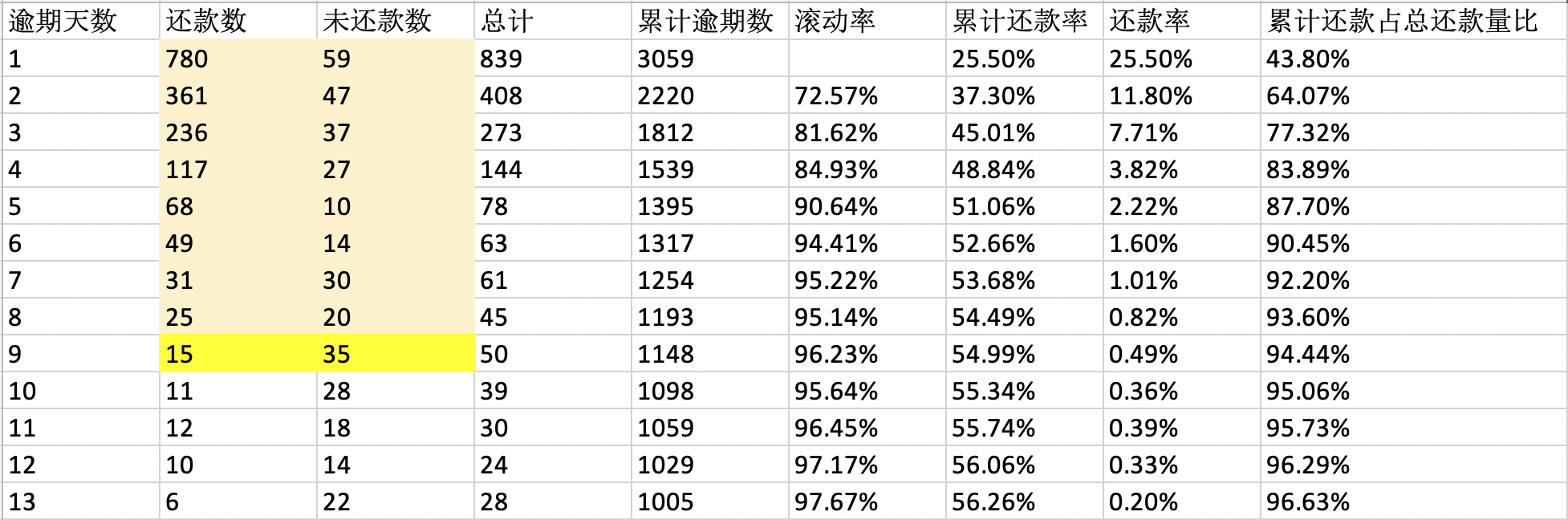
确定时间窗口
- 确定观察期时间
- 主要依赖于建模数据量的要求,如建模样本中的坏至少有500个
- 避开特殊时间,如春节导致的节假日效应
- 避开巨大的产品变动
- 确定表现期时间长度:帐龄分析(Vintage)
- 帐龄(Mob)=账单结算月份 - 账户开立月份,单位:月份
- 统计各个帐龄上,表现为坏账户的累计占比情况,寻找占比增长稳定的月份
- 长度上会按季度选择,如6、9、12、15个月等,传统银行一般表现期在12个月以上,互联网产品会短于一年,现金贷产品一般10天左右就足以表现出坏。
设计子模型
- 子模型细分的原因
- 行为表现本身的差异化
- 让模型更稳定
- 基于业务经验的子模型
- 新老客户
- 产品类型:payday,消费贷,车贷…
- 还款方式:等本等息,先息后本…
- 基于数据驱动的子模型
- 决策树
衍生变量
申请评分
- 传统银行:信贷申请信息+央行信用报告
- 互联网产品:信贷申请信息+手机通讯信息+app操作信息+第三方数据
行为评分
- 传统银行:贷后数据+央行信用报告+历史逾期情况+当前负债情况+帐龄+个人信息
- 互联网产品:贷后数据+手机通讯信息+app操作信息+第三方数据
注意事项
- 基于现有数据衍生出足够多的变量,如:计算对应的均值、最大值、最小值和比例
- 需要在时间维度衍生变量,如:基于逾期状态可以衍生出最近3个月最大逾期状态、最近6个月最大逾期状态
- 由于金额类变量不稳定且易手通货膨胀等因素影响,因此金额累变量需要通过计算比例以消除该问题,如:根据贷款金额和收入计算贷款金额收入比
- 不能衍生无法解释,没有业务含义的变量
- 特殊取值需要定义特殊值,如缺失和未知需要分开,比例型变量中分母为0或缺失和分子为缺失时需要分开赋值。
抽样与权重设置
随机抽样
- 好/坏样本不足5k:不抽样,全部用于建模。
- 好/坏样本大于5k:各抽取5k用于建模。5k是经验值,也可以坏样本全部入模,好样本部分抽取。
设置权重
- 不抽样:权重均为1
- 抽样:
- 好权重 = (好全量+不确定全量) / 好样本量量
- 坏权重 = 坏全量 / 坏样本量
Train & Test
Train 70%, Test 30%.
细分箱
采用传统评分卡建模方式是不采用原始值进行回归拟合的,而是将原市值转换成WOE(证据权重,Weight of Evidence)值进行logistic回归。信息值(Information Value)是反映各变量对于好坏样本识别能力的指标。
变量细分箱
计算WOE值前,先需要将变量分成若干个栏位。
- 对于字符型变量,一般每个取值都作为单独的一栏。
- 对于数值型变量,有多种划分方式,建议采用CART决策树。为了保证分箱稳定,每个分箱一般不小于5%。
计算WOE值与IV
$$ WOE_i = ln( \frac{Good_i}{Good} / \frac{Bad_i}{Bad} ) $$
WOE值越大,表明该栏位中好样本占比越高。
$$ IV = \Sigma( \frac{Good_i}{Good} - \frac{Bad_i}{Bad} ) * WOE $$
IV越大,则该变量在好坏样本上的区分力越大。
Goodi 是第i 个栏位对应的好样本数,Good是好样本总量,Badi是第i 个栏位对应的坏样本数,Bad是坏样本总量。

变量筛选
- 剔除IV值过低的变量:普遍当变量IV值低于0.02时,认为该变量对于好坏样本的区分能力较弱,可以剔除。该阈值是经验值,在实际操作中,根据候选变量的情况可进行调整。
- 剔除变量趋势和业务逻辑不符的变量:所有变量的WOE值变动趋势要复合业务逻辑,如果WOE值不符合该趋势变动,则该变量不能用。如已婚人士的WOE值应高于未婚人士。
- 剔除粗分箱后IV值下降超过30%的变量:如果在变量分箱过程中,强制合并两个有差异的栏位,导致IV下降过多,则最后的模型评分容易导致排序性混乱或不稳定。
- 剔除集中度过高的变量:如某一取值分箱的占比超过98%。
粗分箱
之前的WOE值的分箱是在自动分箱(细分箱)的结果上计算的。因此需要依据细分箱的WOE结果,结合业务和数据分布对该变量进行粗分箱调整。目前,由于收到监管机构要求可解释性,绝大部分金融机构都是手动调整变量分箱。
变量分箱主要从以下方面考虑:
- 考虑WOE值是够单调递增或递减,特殊情况下可以接受U型或倒U型。
- 每个变量栏位上的客户数不能太少,否则不稳定。
- 每个变量栏位上的WOE值要能区分开,否则最后每个栏位得分相近没有区分度,相邻栏位的WOE值相差至少0.1。粗分箱的栏位建议在5个左右。
- 从细分箱到粗分箱到过程中,IV不能下降太多(10%),否则会流失变量的区分能力。
- 粗分箱的栏位值要结合变量的业务含义。如月份类型的变量可以考虑3个月,6个月等作为栏位边界值;而百分比变量则可以考虑在25%,33%,50%等值作为栏位的边界值。

转换WOE值
WOE值转换是把各变量个栏位上的取值转换为对应的WOE值。之后的logistic回归拟合将采用WOE值。
转换完WOE之后,如果候选变量依然较多,可以从变量池内所有可能的变量中,初步确定最有预测能力的变量组合。采用的方法有:使用xgboost计算feature importance,采用重要的变量和逐步判别法等。
Logistic回归
- Logistic回归系数必须为负数:这是因为最后的评分会算到每个变量栏位上,为了保证每个变量的栏位趋势得分符合业务逻辑,所以所有入模变量的回归系数必须均为负数。
- Logistic回归系数的P值必须通过检验:普遍P值不能高于0.05,当模型受到局限性时,可以放宽至0.1。
- 方差膨胀系数(variance inflation factor)必须通过检验:入模变量间不能存在相关性,因此需要对这部分变量进行VIF检验。普遍要求入模变量的VIF不超过4,当模型受到局限性时,可以放宽至10。同时,因为入模变量最后是转换成WOE值去拟合,因此部分变量会存在业务含义看上去具有相关性,但是VIF通过检验的情况,这时可以进行一定的取舍。
- 尽量选择变量栏位、维度多样性,业务含义直观的变量:在候选变量充足或者有几个变量贡献相当但是不能兼容时,尽量选择变量栏位、维度多样性和业务含义直观的变量,这一方面能使模型更具有区分力和稳定性,也能使模型具有更好的解释性。
评分标准化
评分转换逻辑
需要设置标准分,标准odds和PDO三个参数,分数需取整。通常通过假设的方法求解A和B。假设500分时,对应的odds是1,每20分odds翻倍,则原公示可表达为
|
|
解得A=500,B=28.85。
通常把A称为标准评分,标准评分对应的odds称为标准odds(这里是1),而每多少分对应的odds翻两倍称为PDO(Points to Double the Odds,这里是20)。标准评分,标准odds和PDO都可以根据情况修改。
评分卡生成逻辑
评分卡标准化过程,需要从logistic的计算公式出发:
$$ P_1 = \frac{1}{1+e^{-Z}} $$, 其中$$ z = \alpha + \beta_1 x_1 + \beta_2 x_2 + … + \beta_n * x_n $$
推导公式可获得:$$ z = -ln(\frac{P_0}{P_1}) = -ln(odds) $$
此时,我们可认为ln(odds)和变量X之间是线性关系。
$$ Score = A + B ln(odds) = A - B z $$
每个变量各栏位的评分
$$ X{11tmp} = -B 系数1 WOE{11},\ X{12tmp} = -B 系数1 WOE{12}\ \ …$$
$$ X{21tmp} = -B 系数2 WOE{21},\ X{22tmp} = -B 系数1 WOE{22}\ \ …$$
每个特征的最小得分求和
$$ summin = \Sigma{X1{tmpmin} + X2{tmpmin} + … + Xn_{tmpmin}} $$
常数项处理
$$ avgscore = (A - B * 系数0 + summin) / n $$
每个变量分栏的最终得分
$$ X{11}=round(X{11tmp} - X1_{tmpmin} + avgscore) $$
$$ X{12}=round(X{12tmp} - X1_{tmpmin} + avgscore) $$
验证模型
- 数据集:
- Train:建模数据
- Test:验证数据
- OOT(Out Of Time):选取建模样本时间之后的另外一个时间点验证
- 统计指标:
- 区分能力:KS,ROC,Gini等
- 综合表现:评分排序性
- 稳定性:PSI
区分能力
- KS(Kolmogrov-Smirnov)值:取出每个分数上累计坏样本占比和累积好样本占比的最大差值。该值越大越好,普遍认为当KS大于30%时,模型具有区分能力;当KS值大于50%时,模型具有较好的区分能力。
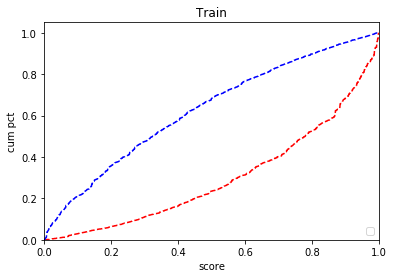
- ROC曲线(Receiver Operating Characteristic Curve):累计好样本占比对应累计坏样本占比曲线。AUC(Area Under Curve)是该曲线下面积。该值越大越好,普遍认为当AUC大于70%时,模型具有区分能力;当AUC值大于80%时,模型具有较好的区分能力。
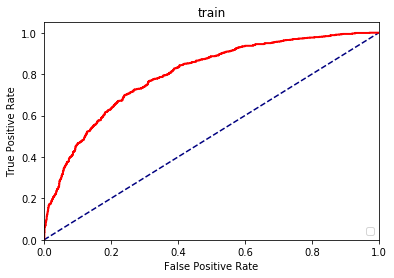
- Gini = 2 * ROC - 1,该值越大越好。
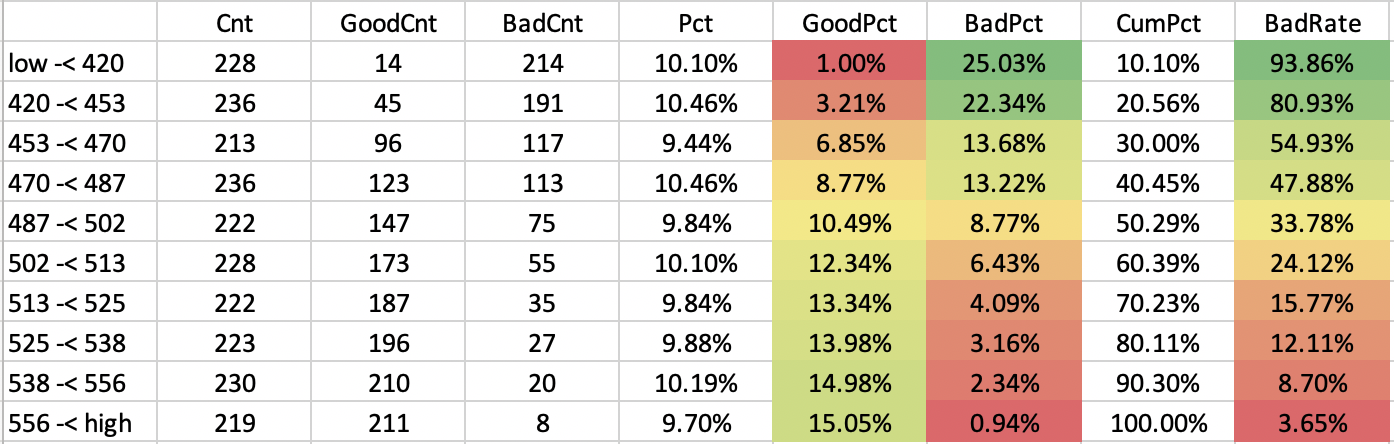
评分排序性
评分排序性是模型评分能力的综合考量。评分结果应该是随着分数的增加,坏账率应该越来越低,同时在每个评分点上,人数占比也要均匀分开,单个评分点上的人数占比不能大于5%。一般会把评分结果按样本数评分成十等份,分别计算其对应的好/坏样本数、坏账率等。
模型稳定性
通过传统评分模型获得结果的一大优势就是稳定性,评分稳定性通过PSI(Population Stability Index)体现。
$$ PSI = \Sigma{ (\%test_i - \%train_i) * \ln(\%test_i / \%train_i)} $$
对最终的评分计算PSI时,先会将Train上的数据集根据样本数平分成十等份,%Traini即对应分数区间上人数占比,在分数区间不变的情况下,计算Test数据集的人数占比即为%Testi。同理计算OOT数据集。
PSI值也可以用于变量稳定性的计算,只要将分数区间换成变量的栏位区间即可。
⼀般⽽言,当PSI⼩于0.1时,评分结果非常稳定,当PSI大于0.25时,评分结果不稳定。
模型部署上线
- 模型开发完成后,由技术部⻔门负责模型的部署上线
- 模型开发者需要提供模型开发⽂文档,特别是评分卡内容和变量量取值计算逻辑
- 模型部署上线之后,一般不会直接采用模型结果,普遍让模型独立运行3-6个月,和原来的处理方式做比较,确认结果之后上线。